Ben North, June 2022
Solutions will appear here.
On the TV gameshow Countdown, there’s a round where six number cards are chosen, along with a target number. Contestants have to use some or all of the six numbers to construct an arithmetic expression which evaluates to the target number, or as close as they can get to it. They’re only allowed the four basic operations (addition, subtraction, multiplication and division), and at all stages of evaluation, the result so far must be positive and integer.
There was some recent interest in this game in our house, and, while realising that I was not going to be the first person to think about this, I wanted to explore how you could write a computer solver.
The approach I took was to try to construct a parse tree for the expression. Initially I thought a binary tree would be a good place to start, followed by a refinement pass to produce an n-ary tree, by collapsing, for example, “(3 + 4) + 5” into “3 + 4 + 5”. Also, the ordering of an operation node’s children is unimportant. I was hoping there would then be some way to throw out duplicate trees.
After a bit more thought, though, it seemed cleaner to start directly with the generation of all possible n-ary trees. Some care is needed to be precise about what this means. The paper
is concerned with dendrograms, and gives a useful classification of the different ways of thinking about “all trees”. It talks about whether a tree is binary or general-n-ary, whether the leaf nodes are “labelled” or “unlabelled”, and whether the nodes are “ranked” or “unranked”. Our situation corresponds to what Murtagh calls "labelled, non-ranked, non-binary" trees.
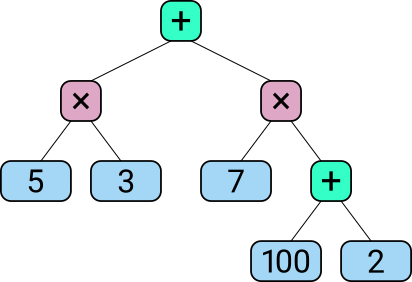
To enumerate the possible Countdown expressions without duplication, the operation (i.e., non-leaf) nodes have to alternate between “+” and “×” as you travel from the root to the leaves. The root operation node can be either kind. This example's root node (at the top of the diagram, since computer scientists draw their trees upside-down) is an addition operation:

Subtraction and division are handled by tagging each non-root node to say whether its value is used by its parent in a non-inverted or inverted sense. An inverted child of a “+” node is actually subtracted, and an inverted child of a “×” node is actually divided by. It is not permitted for all children of a node to be inverted.
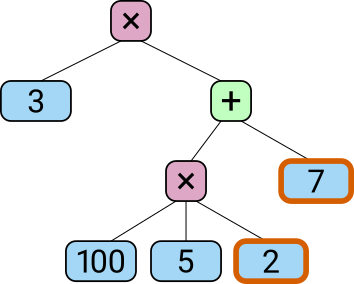
In this example, inverted number nodes are shown like this:
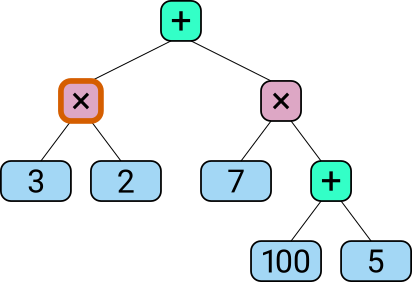
And another example, where a whole subexpression is inverted (its operator node is shown like this):
The question then is how to generate all n-ary trees with up to six leaf nodes. Murtagh describes a recursive solution to this problem, and gives the total number of such trees in the paper's Table 2 — there are 3020 of them.
Given this large set of trees, we can generate all possible Countdown expressions with a few extra steps. For example, suppose we have a 4-leaf-node tree.
We can choose the way the four leaf node labels correspond to four of the six number cards in 6-choose-4 = 15 ways.
For each such choice, we can either assign the root node to be a “+” node or a “×” node.
For each such choice, we alternate between “+” and “×” as we follow each path to a leaf node. With that done, we look at each operation (branch) node in turn. For each one, we list all proper subsets of the set of that node’s children. Then we loop over the Cartesian product of choices of subsets for all operation nodes.
For each operation node and its chosen subset of children, we mark that subset of that node’s children as “inverted” and the rest of its children as “non-inverted”. The requirement that we choose a proper subset ensures we satisfy the rule that we can’t have an operation node all of whose children are inverted.
Finally we can evaluate the expression and test whether the result matches the target. We also check that it is possible to evaluate the expression such that all intermediate results are positive integers.
For the implementation, I split the task after generating the k-leaf-node n-ary trees and choosing which k cards from the complete set of six cards they applied to, and dumped representations of those trees as ‘programs’ for a stack-based machine. The instructions this machine understands are “push card's value onto the stack” and “pop the top N values off the stack, combine them with OP, and push the result back on the stack”. The operation OP can be addition or multiplication. The program is then equivalent to the Reverse Polish Notation (postfix) representation of the expression.
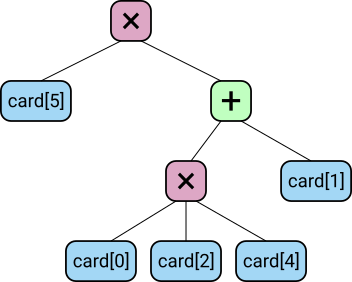
The exploration of the choices of which inputs to invert is deferred until evaluation time. At the time the programs are generated, we don't know the values of the cards, so the program refers to card[0] up to card[5], leaving the values to be filled in at evaluation time.
For example:
That part was done in Python, and resulted in 4659 programs. These programs are hard-coded into a separate C++ program, which interprets them as program templates. It pre-processes the list by copying and then swapping “+” with “×” in the copies. It executes the double-size list of programs by following all the different execution paths arising from the different choices of what subset of each node's children to invert. To ensure we can keep to the rules about always having positive integer intermediate results, it processes all non-inverted arguments before any inverted ones. If the result of any operation fails to be a positive integer, we abandon that execution branch. We also abandon a branch if it involves multiplying by 1. Multiplying by 1 is not strictly against the rules, but it seems cleaner to exclude those solutions.
To wrap this in something suitable for demonstration on the web, I compiled the C++ into wasm using emscripten. A bare JS program takes care of allowing user input of the cards and target number, feeding these to the wasm part, and interpreting the valid solutions in a human-friendly way.
The code is available on GitHub.
YouTube has some examples of unusually difficult numbers rounds:

Make the target 952 from the cards 25, 50, 75, 100, 3, and 6.
The contestant — to much applause — found the solution ((75 × (100 + 6) × 3) − 50) ÷ 25. The tree-based solver finds this solution and also 25 + (75 × (100 + 3) × 6 ÷ 50).

Make the target 813 from the cards 25, 50, 75, 100, 1, and 10.
The contestant found the solution ((25 × (75 − 10)) + 1) × 50 ÷ 100, which the tree-based solver also finds.
I deliberately didn’t look for details of how other solvers worked before doing this. Doing so afterwards, I found that almost everyone else has taken the approach of exploring all valid Reverse Polish Notation (postfix) expressions; for example, this nice analysis by Henriqiue Daitx, and this C implementation by Rachel Evans.
Brute Forcing The Countdown Numbers Game — Computerphile also uses generation of RPN programs. A comment says "The first thing that sprang to mind was a tree-based approach" but didn't elaborate, and replies didn't describe what I did in this project.
Some of these analyses note that there are ways to cut down the search space, which also reduces duplication in the emitted solutions. For example, Tim Hargreaves points out that we need not look at solutions where addition or multiplication expressions have their operands in non-ascending order; Evans's solver also uses this observation.
A solver by David Llewellyn-Jones does take a tree-based approach, using binary trees where all four operators can appear as the non-leaf nodes.
HappySoft's Countdown Numbers game ranks highly in web search results. It handles the case where the target number can not be reached exactly; but it does sometimes miss solutions. For example, it produces an expression giving 950 for the first example above. Its solver is server-side so we can't tell what approach it takes.
To check my solver, I wrote a Python program which repeatedly runs both my solver and one based on Evans's RPN-based one, and compares their solutions. Some care is needed to come up with a canonical representation of a given solution, to know when two solutions, different on the surface, are really “the same”.
Results of this comparison over many thousands of random problems were that all solutions found by my approach were also found by the RPN-based solver, and vice versa. Runtime was pretty similar too. Of the two approaches, the RPN one has the advantage of more obviously being correct in terms of not missing solutions, so it was reassuring that the solution sets matched in all the trials I ran.
The RPN solution did tend to produce duplicate solutions, though. As a cherry-picked example, the problem
when analysed by my solver, has the unique solution
On the other hand, the RPN solver produces the following 15 solutions:
which are all essentially the same.
It’s possible to have two cards with the same number. The tree-based solver described here can produce duplicated solutions if given repeated numbers for the cards. For example, for the problem
(which the DataGenetics blog reports involves the largest intermediate value (99600) of any possible game), my solver gives the two essentially identical solutions
It shouldn't do this.
In the real game, if the target cannot be reached, the winner is the person who can get closest to it. The tree-based solver here does not produce anything if it can't get the target exactly. It should.
An exhaustive study of all possible numbers-round games is possible (and has been done by others). This would provide a better validation than just comparing the behaviour on a few thousand randomly-chosen games.
The code for the tree-based solver (and this write-up) is available on GitHub: